とにかく、M値を完結させて、次に行かなくてはならない。
![]()
カットは福田克之撮影
前回示した前提条件でM値の計算式で計算する。
「M値の計算式
![]()
この式で、16の半飽和組織のそれぞれについて、M値を算出する。
式が出てくると、もうなんだかわからなくなるが、ある数値を計算するために、何が必要とされているのか、という視点でみる。
・Paは、大気圧 100kPa
・Pcは圧変化後の環境圧力(ゲージ圧、kPa)、
要するに潜っている水深をわかりにくく表現している。
Pa+Pc は、潜っている水深の絶対圧のことで、このようにしてわかりにくくして混乱させようという下心のある式である。
潜水している絶対圧(すなわち水深)にB分の1 つまりBの逆数(定数)を×け、定数Aをくわえれば、M値がでる。
水深に定数を乗じて、定数を加えるだけのことだ。Aとか、Bは、少年A、Bのようなもので、仮の呼び名だ。
水深を定数で割り(逆数を掛け)定数を足したのだから、出てきたM値も水深になる。AとBの正体は、a とかb とか言う、生まれ育ちで決まっている。そのa とかb とかは、別の表にしめされている。
空気の場合はA=a B=b だ。なぜこんなまわりくどい、面倒なことをするかというと、ヘリウムを混合した混合ガスでのM値を計算するためだ。
これがM値だ。水深に定数を✕け、定数を足したのだから、M値も水深である。
ところでその水深とはなんだ。それがわからなかった。
ホールデンの2分の1ルールは2分の1の水深だった。30mに潜っていれば、とりあえず10mまでは浮上できる。30m潜っている時のホールデンのM値は10mだ。
だからM値とは、ある水深に潜水している時に、そこまでは、浮上して良い水深なのだ。
ただ。僕がこんらんしたのは、潜水して時間が経過すると、M値が変動すると思ってしまったことで、いちいち計算するのだから、変動するのだろうと思ってしまった。
しかし、式を分析してみれば、変動するのは潜っている水深だけだ。潜っている水深と半飽和組織で、M値は決まっている。つまり、式の定数は半飽和組織で決まる定数だ。a とかb は、半飽和組織によってきまっていて、半飽和組織の表にでてくる。
16通りの各組織も飽和に達してしまえば、それ以上溶けることもない。同様に、最大許容値であるM値も16通りの組織で決まっていて変動はしない。変動するのは、最大許容値に達するまでの溶解分圧の時間経過による変化である。
飽和に達しなければ、そして飽和よりも大きい溶解度であるM値にたっしなければ、その組織は減圧停止不要なのだ。
だからM値が、20mの組織は、20mを超えなければ、いくら時間が経過しても、減圧症にはならない。16通りの組織の中には、M値が9.8mという組織もある。これは、10mでも不活性ガスを貯めこんでゆく。しかし、9.8mの組織は、半飽和時間が長い。たとえば、635分の組織では、その6倍として、63時間も飽和に達するまでの時間が長い。飽和潜水で、完全に飽和するまで時間がかかるのはそのためだ。そして、遅い組織は不活性ガスが排出されるのも時間がかかる。
一方で、たとえば半飽和時間が短い。5分の組織は30分で飽和する。
![]()
表は、中央労働災害防止協会の講習資料寄りの引用
グラフに半飽和組織毎の、水深とM値の相関を示した。半飽和時間が短いほど、グラフは上の方、M値が深くなっている。半飽和時間が長い程、グラフは下の方、M値が浅くなっている事がわかる。繰り返して言うと、半飽和組織の時間が短いほど、グラフの線は、上の方M値は深くなっている。
16通りの組織について、それぞれの減圧スケジュールができるわけで、それをくみあわせて、どの組織もM値を超えないようにしたスケジュールが減圧表である。
半飽和時間が短い組織は浅いところではグラフの線に乗らない。M値に達しないから減圧不要である。長い組織は、浅い水深でも不活性ガスを貯めこんでいるが、なかなか飽和に達しない。M値にも達しない。
そして、不活性ガスの排出は、飽和とM値の間で排出される。
不活性窒素の現在の溶解分圧をしらべて、M値と比較しなければならないから、
溶解窒素の計算式がある。
![]()
これも、当然理解不能である。当該(該当するという意味)つまり求める、その時点での不活性窒素の分圧がPn2であり
それを計算するのに必要な数値が下に示されている。
大気圧は絶対圧にするため。
潜水しているその時点のゲージ圧
その時の窒素濃度
加圧または減圧の速度
時間
半飽和時間
時間とか変化の速度、窒素濃度、半飽和時間が溶解している不活性ガスの分圧を計算するために必要である。
つまり、求める数値は、潜水しているその時間での不活性窒素分圧であり、もちろん一定ではない。この不活性窒素分圧と、M値を比較する。どちらも圧力の単位だから、大きい小さいを比較することができる。
変動している値であり、そのある時点での窒素分圧ががM値よりも小さいことを確認できる。こうして、窒素分圧が常に、すべての半飽和組織でM値を越えないようにして浮上する。
ここまでをまとめると、
M値
エムチと呼びますが、不活性ガスの最大許容値のことです。潜水して時間が経過すると、16通りの組織モデルそれぞれに、潜水する深さに応じて、一定の時間経過で不活性ガスが飽和します。浮上すると、環境圧が下がり、呼吸する気体圧力も減少することで、半飽和組織内の不活性ガスが過飽和になり、飽和していなくても浮上によって飽和になり、M値と飽和との間に圧力差(圧力勾配差)が生じ、不活性ガスは排出に向きます。過飽和になりすぎると気泡化します。どこまで浮上したら、気泡化が起こらないで排出されるか、その最大許容値がM値です。 飽和する値が、各半飽和組織毎に、水深によって異なるのと同様に、M値も水深によって定まります。飽和とM値の間で、ガスは排出されます。M値を越えないように浮上停止をして、ガスを排出しながら浮上するように計算された時間表が減圧表です。

カットは福田克之撮影
前回示した前提条件でM値の計算式で計算する。
「M値の計算式
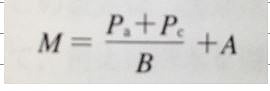
この式で、16の半飽和組織のそれぞれについて、M値を算出する。
式が出てくると、もうなんだかわからなくなるが、ある数値を計算するために、何が必要とされているのか、という視点でみる。
・Paは、大気圧 100kPa
・Pcは圧変化後の環境圧力(ゲージ圧、kPa)、
要するに潜っている水深をわかりにくく表現している。
Pa+Pc は、潜っている水深の絶対圧のことで、このようにしてわかりにくくして混乱させようという下心のある式である。
潜水している絶対圧(すなわち水深)にB分の1 つまりBの逆数(定数)を×け、定数Aをくわえれば、M値がでる。
水深に定数を乗じて、定数を加えるだけのことだ。Aとか、Bは、少年A、Bのようなもので、仮の呼び名だ。
水深を定数で割り(逆数を掛け)定数を足したのだから、出てきたM値も水深になる。AとBの正体は、a とかb とか言う、生まれ育ちで決まっている。そのa とかb とかは、別の表にしめされている。
空気の場合はA=a B=b だ。なぜこんなまわりくどい、面倒なことをするかというと、ヘリウムを混合した混合ガスでのM値を計算するためだ。
これがM値だ。水深に定数を✕け、定数を足したのだから、M値も水深である。
ところでその水深とはなんだ。それがわからなかった。
ホールデンの2分の1ルールは2分の1の水深だった。30mに潜っていれば、とりあえず10mまでは浮上できる。30m潜っている時のホールデンのM値は10mだ。
だからM値とは、ある水深に潜水している時に、そこまでは、浮上して良い水深なのだ。
ただ。僕がこんらんしたのは、潜水して時間が経過すると、M値が変動すると思ってしまったことで、いちいち計算するのだから、変動するのだろうと思ってしまった。
しかし、式を分析してみれば、変動するのは潜っている水深だけだ。潜っている水深と半飽和組織で、M値は決まっている。つまり、式の定数は半飽和組織で決まる定数だ。a とかb は、半飽和組織によってきまっていて、半飽和組織の表にでてくる。
16通りの各組織も飽和に達してしまえば、それ以上溶けることもない。同様に、最大許容値であるM値も16通りの組織で決まっていて変動はしない。変動するのは、最大許容値に達するまでの溶解分圧の時間経過による変化である。
飽和に達しなければ、そして飽和よりも大きい溶解度であるM値にたっしなければ、その組織は減圧停止不要なのだ。
だからM値が、20mの組織は、20mを超えなければ、いくら時間が経過しても、減圧症にはならない。16通りの組織の中には、M値が9.8mという組織もある。これは、10mでも不活性ガスを貯めこんでゆく。しかし、9.8mの組織は、半飽和時間が長い。たとえば、635分の組織では、その6倍として、63時間も飽和に達するまでの時間が長い。飽和潜水で、完全に飽和するまで時間がかかるのはそのためだ。そして、遅い組織は不活性ガスが排出されるのも時間がかかる。
一方で、たとえば半飽和時間が短い。5分の組織は30分で飽和する。
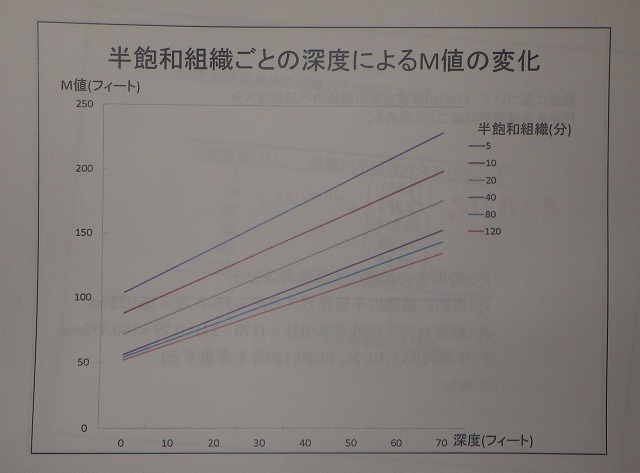
表は、中央労働災害防止協会の講習資料寄りの引用
グラフに半飽和組織毎の、水深とM値の相関を示した。半飽和時間が短いほど、グラフは上の方、M値が深くなっている。半飽和時間が長い程、グラフは下の方、M値が浅くなっている事がわかる。繰り返して言うと、半飽和組織の時間が短いほど、グラフの線は、上の方M値は深くなっている。
16通りの組織について、それぞれの減圧スケジュールができるわけで、それをくみあわせて、どの組織もM値を超えないようにしたスケジュールが減圧表である。
半飽和時間が短い組織は浅いところではグラフの線に乗らない。M値に達しないから減圧不要である。長い組織は、浅い水深でも不活性ガスを貯めこんでいるが、なかなか飽和に達しない。M値にも達しない。
そして、不活性ガスの排出は、飽和とM値の間で排出される。
不活性窒素の現在の溶解分圧をしらべて、M値と比較しなければならないから、
溶解窒素の計算式がある。

これも、当然理解不能である。当該(該当するという意味)つまり求める、その時点での不活性窒素の分圧がPn2であり
それを計算するのに必要な数値が下に示されている。
大気圧は絶対圧にするため。
潜水しているその時点のゲージ圧
その時の窒素濃度
加圧または減圧の速度
時間
半飽和時間
時間とか変化の速度、窒素濃度、半飽和時間が溶解している不活性ガスの分圧を計算するために必要である。
つまり、求める数値は、潜水しているその時間での不活性窒素分圧であり、もちろん一定ではない。この不活性窒素分圧と、M値を比較する。どちらも圧力の単位だから、大きい小さいを比較することができる。
変動している値であり、そのある時点での窒素分圧ががM値よりも小さいことを確認できる。こうして、窒素分圧が常に、すべての半飽和組織でM値を越えないようにして浮上する。
ここまでをまとめると、
M値
エムチと呼びますが、不活性ガスの最大許容値のことです。潜水して時間が経過すると、16通りの組織モデルそれぞれに、潜水する深さに応じて、一定の時間経過で不活性ガスが飽和します。浮上すると、環境圧が下がり、呼吸する気体圧力も減少することで、半飽和組織内の不活性ガスが過飽和になり、飽和していなくても浮上によって飽和になり、M値と飽和との間に圧力差(圧力勾配差)が生じ、不活性ガスは排出に向きます。過飽和になりすぎると気泡化します。どこまで浮上したら、気泡化が起こらないで排出されるか、その最大許容値がM値です。 飽和する値が、各半飽和組織毎に、水深によって異なるのと同様に、M値も水深によって定まります。飽和とM値の間で、ガスは排出されます。M値を越えないように浮上停止をして、ガスを排出しながら浮上するように計算された時間表が減圧表です。